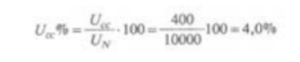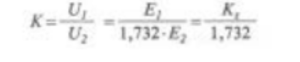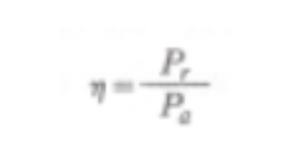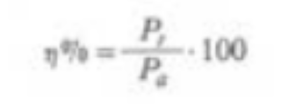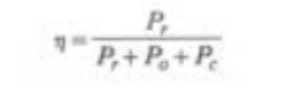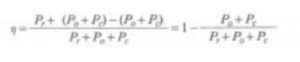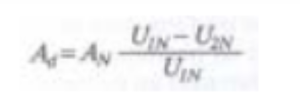L’articolo offre un quadro completo ed aggiornato delle leggi che regolano l’elettrotecnica, leggi che anche un tecnico pratico, quale può essere un installatore, non può esimersi dal conoscere per svolgere razionalmente il proprio lavoro. Parte tre: CARATTERISTICHE FUNZIONALI DEL TRASFORMATORE.

L’inizio dell’articolo è riportato sul fascicolo precedente numero 772.

3.6 – Determinazione della impedenza di corto circuito del trasformatore
La impedenza interna del trasformatore che provoca le variazioni di tensione al secondario può essere determinata sperimentalmente con una prova in corto circuito. Essa è chiamata impedenza di corto circuito del trasformatore. Si dice invece tensione di corto circuito la tensione che applicata ad un avvolgimento con l’altro in corto circuito fa circolare in entrambi la corrente nominale.

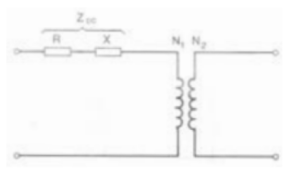
Figura 3.13 – Schema equivalente semplificato del trasformatore reale nel quale si trascurano i parametri in derivazione.

Le variazioni di tensione di un trasformatore già costruito possono essere determinate per via diretta, cioè misurando la tensione ai morsetti secondari quando il circuito secondario è aperto (trasformatore a vuoto) e quando esso è chiuso sul carico, tenendo in entrambi i casi costante la tensione di alimentazione del primario e la frequenza. Questo procedimento implica difficoltà pratiche ed è poco preciso, per cui viene impiegato solo eccezionalmente per trasformatori di piccola potenza, mentre in generale si usano metodi indiretti. Si riprenda la formula che esprime la relazione tra le tensioni primarie e le tensioni secondarie a carico:
U₁ = K · U₂ + K · Z₂ · I₂ + Z₁ · I₁
Se si trascura la corrente a vuoto, è valida la relazione  I₂ = K · I₁, per cui la formula può essere scritta così:
U₁ = K · U₂ + (K² · Z₂ + Z₁) · I₁
Si può perciò considerare come impedenza interna del trasformatore il valore dato dall’espressione:
Z_cc = K² · Z₂ + Z₁
Questa impedenza è detta di corto circuito e nel caso considerato è riferita al primario. La caduta di tensione corrispondente, quando è in gioco la corrente nominale, può essere facilmente determinata con la cosiddetta prova in corto circuito. La prova in corto circuito consiste nel chiudere in corto circuito, ossia con collegamenti di resistenza trascurabile, i morsetti di uno dei due avvolgimenti ed alimentare l’altro con una tensione opportunamente ridotta in modo che negli avvolgimenti circolino le correnti nominali (Figura 3.14).

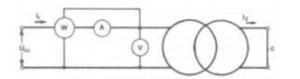
Figura 3.14 – Schema per la prova in corto circuito: W – wattmetro per la misura delle perdite dovute alla corrente; A – amperometro; V – voltmetro; U_cc – tensione di alimentazione ridotta per far circolare le correnti nominali; e – collegamento di corto circuito.

In queste condizioni la tensione U₂ è nulla. La tensione richiesta è di pochi percento di quella nominale. Se si applicasse la piena tensione, la corrente, essendo limitata soltanto dalla impedenza interna del trasformatore, assumerebbe valori molto elevati sopportabili dalla macchina soltanto per tempi brevissimi (dell’ordine del secondo). È quanto succede in esercizio nel caso di corto circuito ai morsetti secondari. La tensione applicata deve invece vincere soltanto l’impedenza propria del trasformatore, ossia è uguale agli effetti risultanti delle cadute ohmiche e delle cadute induttive. Il valore della tensione U_cc è infatti dato da:
U_cc = Z_cc · I_N

essendo I_N il valore nominale della corrente dell’avvolgimento alimentato. Nel circuito di prova devono essere inseriti tre strumenti di misura: un amperometro, un voltmetro ed una wattmetro. In base ai risultati di una prova condotta con I_N si ottengono i valori di U_cc e P_cc in base ai quali è possibile calcolare l’impedenza e le sue componenti resistiva e induttiva. La tensione richiesta per fare circolare la corrente nominale è detta tensione di corto circuito. Si può allora costruire il triangolo rettangolo ABC delle componenti della tensione di corto circuito oppure il triangolo delle impedenze ottenuto dividendo i lati del primo per il valore di I_N (Figura 3.15).

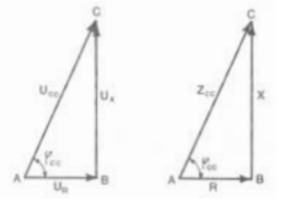
Figura 3.15 – Diagrammi vettoriali delle componenti della tensione di corto circuito (a) e della impedenza relativa (b).

Si tenga presente che la componente resistiva varia con la temperatura. La tensione di corto circuito costituisce uno dei dati nominali del trasformatore ed è normalmente espressa in percento della tensione nominale a vuoto. Ad esempio, se la tensione di corto circuito U_cc = 400 V e la tensione nominale dell’avvolgimento alimentato è U = 10 000 V, la tensione di corto circuito relativa percentuale sarà:

3.7 – Il diagramma di Kapp

La determinazione delle variazioni di tensione in funzione del carico e del suo fattore di potenza può essere fatta per via grafica o mediante formule.

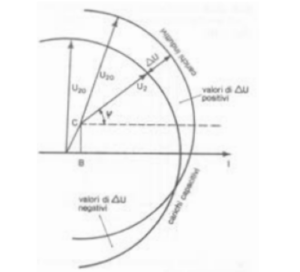
Per poter determinare rapidamente e per via grafica le variazioni di tensione in relazione ai vari fattori di potenza, si può ricorrere al diagramma di Kapp (da tracciare per ogni corrente di carico considerata) i cui cateti risultano OB = (R’₁ + R₂) I₂ e BC = (X’₁ + X₂) I₂ essendo R’₁ e X’₁ rispettivamente la resistenza e la reattanza degli avvolgimenti riportate al secondario. Per la costruzione del diagramma si fa centro successivamente nei due vertici O e C degli angoli non retti del triangolo di Kapp e, con raggio uguale alla tensione a vuoto, si tracciano due cerchi (Figura 3.16). 

Figura 3.16 – Diagramma di Kapp per la determinazione grafica delle variazioni di tensione.

Per avere la variazione della tensione a carico a un determinato cosφ si traccia una semiretta uscente da C facente, con l’asse di riferimento (linea tratteggiata), l’angolo φ (in senso antiorario se si tratta di carico induttivo). Il segmento intercettato in questa semiretta dai due cerchi dà la variazione di tensione cercata (∆U). In pratica però si preferisce ricorrere a formule approssimate, dedotte con qualche semplificazione dal diagramma di Kapp, poiché la costruzione del diagramma stesso, nel caso dei trasformatori, non consente sufficiente precisione dato che la variazione di tensione è sempre una piccola percentuale della tensione a vuoto. Per il calcolo delle variazioni di tensione e le percentuali (∆U/%), le norme CEI consigliano la seguente formula:

ove U_R e U_x sono le cadute percentuali rispettivamente ohmica e induttiva date da:

dove:
U_cc = tensione di corto circuito;
U_N = tensione nominale dell’avvolgimento alimentato;
φ_cc = angolo fra tensione e corrente in corto circuito;
φ = angolo di fase del carico alimentato.
La formula suddetta può essere facilmente impostata sui piccoli calcolatori tascabili dotati di modesta memoria.

3.8 – Trasformatori trifasi
Un trasformatore trifase è costituito da un nucleo magnetico con tre colonne sulle quali sono avvolti gli avvolgimenti primario e secondario.

Gli avvolgimenti possono essere collegati a triangolo, stella e zig-zag. Poiché le reti di trasmissione e di distribuzione sono trifasi, l’uso di trasformatori trifasi è molto diffuso. In linea di principio, il banco di trasformazione può essere anche costituito da tre trasformatori monofasi opportunamente collegati tra loro ma, per ragioni di costo, questa soluzione è adottata molto raramente. Nella figura 3.17 è rappresentato uno schema di inserzione che può essere realizzato usando trasformatori monofasi.

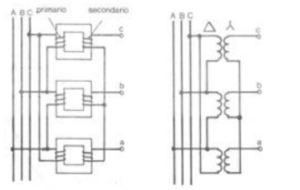
Figura 3.17 – Schema di inserzione di tre trasformatori monofasi per realizzare un banco trifase, collegamento triangolo/stella.

Un trasformatore trifase è costituito da un nucleo avente tre colonne, su ciascuna delle quali sono disposti gli avvolgimenti primario e secondario (Figura 3.18).

Figura 3.18 – Parti fondamentali di un trasformatore trifase.

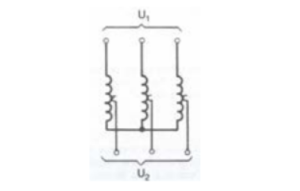
Gli avvolgimenti possono essere collegati tra loro a stella, a triangolo o a zig-zag (Figura 3.19).

Figura 3.19 – Collegamenti degli avvolgimenti trifasi: a – triangolo; b – stella; c – zig-zag.

I collegamenti del secondario possono essere uguali o diversi da quelli del primario, per cui, in teoria, si possono avere varie combinazioni di collegamenti. La scelta dipende da numerosi fattori, ma soprattutto dalla funzione della macchina e dalla sua
posizione nella rete. Nei trasformatori della rete di distribuzione che effettuano la riduzione da media a bassa tensione, è opportuno che l’avvolgimento primario sia a triangolo. Per trasformatori di piccola potenza (100 kVA) si preferisce sovente ricorrere al collegamento a stella sulla media tensione e al collegamento a zig-zag sulla bassa tensione.

Rapporti fra le tensioni nei trasformatori trifasi
Il rapporto di trasformazione di un trasformatore trifase è il rapporto tra le tensioni concatenate primaria e secondaria a vuoto.

Se il primario e il secondario hanno collegamenti diversi, il rapporto fra le tensioni a vuoto ai morsetti non è uguale al rapporto fra i numeri delle spire primarie e secondarie avvolte su una colonna. Esso dipende infatti dai collegamenti adottati perché, come è noto, a ciascun tipo di collegamento corrisponde una determinata relazione fra le tensioni concatenate e le tensioni di fase. Si consideri ad esempio un trasformatore con primario a triangolo e secondario a stella (Figura 3.20) e si indichino con E₁ e E₂ le tensioni a vuoto rispettivamente di una fase del primario e di una fase del secondario e con U₁ e U₂ le tensioni concate nate rispettivamente del primario e del secondario.

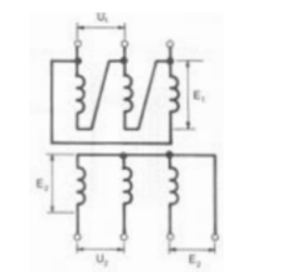
Figura 3.20 – Rapporti tra le tensioni di fase e di linea in un trasformatore con primario a triangolo e secondario a stella.

Avremo al primario (collegato a triangolo) U₁ = E₁ mentre al secondario U₂ = √3 ⋅ E₂ = 1,732 ⋅ E₂. Pertanto, il rapporto fra le tensioni a vuoto ai morsetti sarà in questo caso: 

Poiché nei trasformatori trifasi il rapporto di trasformazione deve intendersi fra tensioni concatenate (si indica con la lettera K), esso non corrisponde al rapporto (Ks) tra il numero delle spire primarie (N1) e secondarie (N2). Ciò significa che nel caso considerato per avere ai morsetti una determinata tensione occorre realizzare l’avvolgimento primario con un numero di spire maggiore di 1,732 volte quello di un trasformatore avente collegamenti uguali (ad esempio, stella/stella). Nella tabella 3.1 sono indicati i rapporti di fase che si debbono adottare per avere un determinato rapporto di trasformazione fra le tensioni ai morsetti, per le combinazioni di collegamenti più usate.

Tabella 3.1 – Simboli grafici e letterali e rapporti spire per colonne in relazione al tipo di collegamento degli avvolgimenti.

Si ricordi che anche per i trasformatori trifasi le tensioni nominali sono quelle corrispondenti al funzionamento a vuoto, secondo quanto prescritto dalle vigenti norme CEI.

Scelta dei collegamenti per i trasformatori trifasi
La scelta dei collegamenti dipende da esigenze di esercizio e da considerazioni economiche.

La scelta dei collegamenti dei trasformatori trifasi dipende da un certo numero di fattori. Sotto l’aspetto tecnico è determinante il tipo di esercizio previsto per la rete. Per esempio, nelle reti di distribuzione a tre fili con neutro, essendo necessario avere un centro stella accessibile, si possono impiegare soltanto avvolgimenti collegati a stella o a zig-zag. Nei trasformatori con primario a triangolo e secondario a stella (o primario a stella e secondario a zig-zag), gli squilibri di carico (fasi non ugualmente caricate) si ripercuotono meno sulla linea di alimentazione primaria. I collegamenti degli avvolgimenti possono essere indicati anche con lettere qualora ciò risulti comodo (ad esempio sulle targhe delle macchine). Secondo le norme CEI, si indicano con lettere maiuscole i collegamenti relativi all’alta tensione e con lettere minuscole quelli della bassa tensione. Le lettere da usare per i vari collegamenti sono riportate nella tabella 3.1. Ad esempio, una macchina media tensione/bassa tensione con primario a triangolo e secondario a stella con il centro accessibile sarà indicato con le lettere D e yn. Agli effetti economici si può dire che in linea di massima gli avvolgimenti a triangolo sono un po’ più costosi di quelli a stella, dovendo impiegare conduttori di diametro minore e dovendo avvolgere un maggior numero di spire. L’avvolgimento a zig-zag richiede, a parità di tensione, un numero di spire secondarie maggiore del 15% di quello di un avvolgimento a stella.

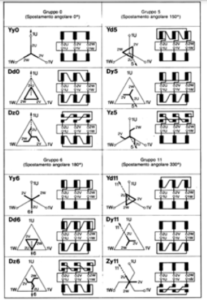
Gruppi angolari dei trasformatori trifasi
Nei trasformatori trifasi il sistema delle tensioni secondarie può essere sfasato rispetto a quello delle tensioni primarie. Ogni trasformatore è perciò caratterizzato da un gruppo angolare.

Nei trasformatori trifasi ha grande importanza l’eventuale spostamento di fase tra il sistema delle tensioni di bassa e il sistema delle tensioni di alta. Ciò interessa agli effetti del parallelo dei trasformatori, come vedremo fra breve. Nei trasformatori monofasi e nei trasformatori trifasi a collegamenti omonimi (stella/ stella, triangolo/triangolo) le tensioni di bassa possono soltanto essere o in fase o in opposizione di fase (cioè spostamento di fase rispettivamente 0°, oppure 180°) rispetto alle tensioni di alta. Ciò in relazione al senso di avvolgimento dei conduttori e alla denominazione attribuita ai morsetti degli avvolgimenti. Invece nei trasformatori trifasi a collegamento misto (stella/ triangolo, triangolo/ stella, stella/ zig-zag) questo spostamento angolare non può mai essere né 0° né 180°, ma risulta multiplo dispari di 30°. Esaminando vettorialmente tutte le combinazioni di collegamenti trifasi, risulta in definitiva che si possono avere (comprendendo lo spostamento 0°) dodici distinti valori di spostamento angolare, che variano di 30° in 30°. Essi si considerano sempre ritardi della bassa tensione rispetto all’alta tensione e si indicano con la denominazione convenzionale di Gruppo 0 (12), 1, 2… 11, corrispondente alla lettura dell’ora su di un quadrante d’orologio nel quale la sfera lunga (minuti) rappresenta la forza elettromotrice indotta nell’avvolgimento di alta tensione e sta sullo 0, mentre la sfera corta (ora) rappresenta la forza elettromotrice indotta nell’avvolgimento di bassa tensione. Le norme CEI raccomandano come normali i gruppi 0 e 11 (spostamenti angolari 0° e 330° rispettivamente). Nella tabella 3.2 sono riportati i simboli grafici e gli schemi di alcune tra le combinazioni più comuni con l’indicazione dell’indice orario. 

Tabella 3.2 – Gruppi di collegamenti nei trasformatori trifasi.

3.9 – Potenza dei trasformatori
La potenza nominale di un trasformatore è data dal prodotto della tensione nominale a vuoto e della corrente nominale di uno dei due avvolgimenti. Nel caso di macchine trifasi si deve moltiplicare anche per √3 = 1,732.

La potenza dei trasformatori è espressa in voltampere (o multipli). Le vigenti norme CEI definiscono come potenza nominale (AN) per i trasformatori monofasi il prodotto della tensione nominale a vuoto (UN) per la corrente nominale (IN) dell’avvolgimento considerato: A_N = U_N · I_N

Essa esprime perciò una potenza apparente ed è la stessa per entrambi gli avvolgimenti. Questa definizione, che è puramente convenzionale, è molto comoda dal punto di vista del dimensionamento se si tiene presente che il riscaldamento delle parti di un trasformatore è causato dalle perdite che in esse hanno luogo. Perciò una macchina può essere sottoposta ad una tensione e i suoi avvolgimenti possono essere percorsi da correnti di valore determinato, indipendentemente dal fatto che il secondario fornisca o meno una potenza attiva. Ad esempio, l’avvolgimento di un trasformatore monofase con potenza nominale di 100 kVA e previsto per una tensione nominale di 500 V, potrà essere percorso al massimo da una corrente di 200 A e ciò indifferentemente sia che la potenza attiva risulti di 10 kW (quando si avesse cos φ = 0,1) o di 80 kW (cos φ = 0,8) o di 100 kW (cos φ = 1). La potenza nominale, come sopra definita, rappresenta una semplificazione sia per il costruttore che per l’utilizzatore; quest’ultimo infatti, essendo le reti funzionanti a tensione praticamente costante, per controllare che il trasformatore non venga sovraccaricato non ha che da misurarne la corrente assorbita. Occorre anche avere sempre presente che la potenza nominale non deve essere confusa con la potenza apparente effettivamente erogata dal secondario; quest’ultima è sempre data dalla relazione: A₂ = U₂ · I₂
dove:
U₂ · I₂ = rispettivamente la tensione ai morsetti secondari a carico e la corrente erogata al circuito esterno. Pertanto, questa potenza differisce dalla potenza nominale di tanto quanto la tensione a carico U₂ differisce dalla tensione a vuoto U₂₀ mentre I₂ può coincidere con I_2N. Per i trasformatori trifasi la potenza nominale (A_N) è data da tre volte la potenza di una singola
colonna. Facendo riferimento alle tensioni concatenate e alle correnti di linea essa risulta: A_N = √3 · U_N · I_N

3.10 – Perdite e rendimento
Le perdite che si hanno in un trasformatore sono le perdite a vuoto e le perdite dovute al carico.

Le perdite a vuoto sono quasi totalmente localizzate nel nucleo magnetico che, come già precisato, è sottoposto a magnetizzazione variabile. Esse si distinguono in perdite per isteresi e perdite per correnti parassite e dipendono dalla induzione e dalla frequenza. Le perdite dovute al carico sono principalmente localizzate negli avvolgimenti e dipendono dal quadrato delle correnti che in essi circolano (legge di Joule). Dipendono dalla temperatura in quanto la resistività dei conduttori varia con questa. Il rendimento (ƞ) di un trasformatore è dato dal rapporto fra la potenza attiva resa (P_r) e la potenza attiva assorbita (P_a).

In forma percentuale il rendimento risulta:

La potenza assorbita può anche essere espressa come somma della potenza resa e dalle perdite nel ferro P_o (per isteresi e correnti parassite) e nel rame P_c (per effetto Joule): P_a = P_r + P₀ + P_c
Il rendimento si può anche esprimere così:

Con un semplice artificio algebrico che consiste nell’aggiungere e togliere P₀ + P_c al numeratore si può anche scrivere:

che si presta più facilmente ad un corretto calcolo del rendimento partendo dal valore delle perdite. È importante notare che le perdite a vuoto rimangono praticamente costanti mentre, le perdite nel rame variano con il carico. Così un trasformatore che abbia 600 W di perdite nel ferro e 2 000 W di perdite negli avvolgimenti a pieno carico, a metà carico avrà ancora 600 W di perdite nel ferro e: 2 000 (1/2)² = 2 000 / 4 = 500 W di perdite negli avvolgimenti.
Da ciò deriva che la migliore economicità di esercizio di un trasformatore dipende anche dal rapporto fra le perdite. Si considera, ad esempio, un trasformatore di una cabina di distribuzione cittadina, alimentante cioè un gruppo di fabbricati civili: esso deve funzionare a pieno carico soltanto per alcune ore al giorno, mentre per il rimanente tempo funziona a vuoto o a carico molto ridotto. In questo caso interessa poco il rendimento a pieno carico, ma interessa che le perdite a vuoto, sempre presenti, siano le minime possibili. Nel caso invece di un trasformatore per uno stabilimento industriale che sia destinato a lavorare a carico otto o dodici ore al giorno e venga staccato dalla rete alla notte, è più conveniente avere il massimo rendimento a pieno carico o a carico ad esso vicino (ad esempio a 3/4 del pieno carico).

3.11 – Trasformatori unificati
I trasformatori unificati da distribuzione rappresentano una serie di macchine di potenza diversa con caratteristiche funzionali e costruttive adatte per la maggiore parte degli impieghi.

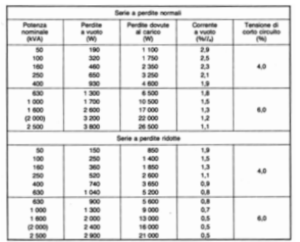
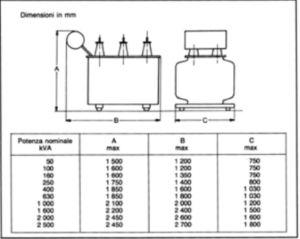
Data la grande diffusione dei trasformatori da distribuzione, il CEI ha provveduto alla unificazione delle macchine in olio. I trasformatori hanno l’avvolgimento di alta tensione munito di prese in modo da adattare la tensione di alimentazione nel campo ± 2 · 2,5%. Per quanto riguarda le tensioni primarie, sono stati unificati i valori di 10-15 e 20 kV che sono i più diffusi sulle reti di distribuzione a media tensione. La tensione secondaria nominale (a vuoto) è per tutte le macchine di 400 V, con neutro accessibile in modo da poter disporre di una tensione di fase di 230 V (a vuoto). I collegamenti unificati sono il triangolo per il primario e la stella per il secondario. Per le macchine di potenza ≤ 160 kVA è anche ammesso il collegamento a stella sul primario con il secondario a zig-zag. Nella tabella 3.3 sono riportati i dati nominali normalizzati di queste macchine, mentre nella tabella 3.4 sono indicate le dimensioni massime di ingombro normalizzate. Il CEI ha previsto due serie normalizzate, una a perdite normali e l’altra a perdite ridotte.

Tabella 3.3 – Caratteristiche nominali dei trasformatori MT/BT unificati dal CEI.

La seconda serie è evidentemente più pregiata (rendimento più elevato) e le macchine sono più costose di quelle della serie a perdite normali in quanto sia le perdite a vuoto che quelle a carico sono ridotte nella misura del 21 ± 24%. La giustificazione della disponibilità di due serie deriva dal fatto che le perdite costituiscono un onere economico in quanto sul tempo corrispondono ad energia dissipata ma comunque prodotta o pagata. Con l’aumento del costo delle fonti d’energia (petrolio, carbone, ecc.) può risultare economicamente conveniente utilizzare macchine più costose, ma le cui perdite comportano successivamente oneri minori. Per quanto riguarda le tensioni di corto circuito è stato fissato il 40% per le macchine fino a 400 kVA e del 6% per le macchine di potenza superiore. Di minore importanza è il valore della corrente a vuoto che è sempre molto picco la rispetto alla nominale. 

Tabella 3.4 – Dimensioni di ingombro massime dei trasformatori MT/BT unificati dal CEI.

3.12 – L’isolamento dei trasformatori
Generalità
L’isolamento dei trasformatori è sottoposto alla tensione di esercizio ed a sovratensioni temporanee. Esso deve essere in grado di sopportarle senza danneggiarsi rapidamente.

I trasformatori sono sottoposti in esercizio a sollecitazioni elettriche che tendono a deteriorare in modo più o meno rapido gli isolanti. Per affrontare il problema in modo razionale, conviene fare distinzione tra le diverse tensioni elettriche che vi possono riscontrare in rete:
– tensione di esercizio: è la tensione che il trasformatore deve sopportare in continuazione per tutta la sua vita;
– sovratensioni temporanee: sono quelle che si verificano occasionalmente e possono essere dovute al distacco dei carichi, a manovre di interruttori, a guasti in rete, a scariche atmosferiche, ecc..
Si tratta in genere di fenomeni di breve durata ma di ampiezza più elevata della tensione di esercizio. Ad esempio, quelle di origine atmosferica hanno durate dell’ordine delle centinaia di microsecondi e ampiezza anche di 6 volte la tensione nominale. Le parti isolanti delle macchine interessate alle tensioni sopra elencate sono gli isolamenti tra spire, verso massa e tra gli avvolgimenti. La scelta degli isolanti e del loro spessore dipende fortemente dal tipo di macchina (a secco, in olio) e dalle tensioni in gioco. La verifica dell’efficacia dell’isolamento viene effettuata in sede di collaudo su tutti i trasformatori di nuova costruzione eseguendo le prove previste dalle norme CEI in vigore. Durante l’esercizio non è in genere necessario effettuare ulteriori prove purché i trasformatori vengano sottoposti alle operazioni di manutenzione ordinaria di cui si fa cenno nel Capitolo 5.

Tensioni di prova degli avvolgimenti
Gli avvolgimenti dei trasformatori vengono sottoposti a prove di isolamento secondo le norme CEI.

Le norme CEI prescrivono per i trasformatori di potenza una serie di prove di isolamento. Limitatamente alle macchine destinate alle reti di distribuzione a bassa e media tensione valgono le brevi considerazioni seguenti. È innanzitutto da precisare che le tensioni di prova sono riferite alla cosiddetta tensione massima del sistema (U_m), ossia la massima tensione concatenata che può verificarsi in servizio normale sulla rete considerata. Per i trasformatori essa risulta più elevata di quella nominale (U_n), come si può rilevare dalla tabella 3.5.

Tabella 3.5 – Tensioni nominali, massime dei sistemi e di prova per gli avvolgimenti dei trasformatori.

Per le tensioni nominali delle reti a media tensione il rapporto U_m / U_n è intorno a 1,2. Per la bassa tensione si assume per U_m il valore minimo di 1,1 kV in modo puramente convenzionale. Come precedentemente ricordato, gli avvolgimenti vengono sottoposti a prove di isolamento. La tecnica di queste prove esula dagli scopi di questo volume e ci si limita pertanto ad un breve cenno sulle prove a frequenza industriale che vengono eseguite su tutte le macchine. Una prima prova è quella di tensione applicata tra ciascun avvolgimento e gli altri collegati a massa. Più precisamente, tutti i morsetti dell’avvolgimento in prova vengono collegati tra loro e la tensione viene applicata come indicato ad esempio nella figura 3.21 che si riferisce al caso di un trasformatore trifase. La prova va effettuata successivamente su entrambi gli avvolgimenti. Il valore delle tensioni di prova, la cui frequenza è solitamente di 50 Hz, è dato dalla tabella 3.6, mentre la durata convenzionale è di 60 s. Una seconda importante prova è quella a tensione indotta, che permette di verificare l’isolamento tra le spire. Il trasformatore viene alimentato come in servizio ma utilizzando una sorgente di tensione a frequenza più elevata della nominale per evitare i fenomeni di saturazione del nucleo che si verificherebbero a 50 Hz dato che la tensione di prova è più alta della nominale. Si ricorda a questo proposito che le f. e.m. di auto e mutua indu zione sono date dalla formula: e = – 4,44 · f · ɸ e che il flusso è proporzionale all’induzione magnetica nel nucleo. Per evitare la saturazione è quindi sufficiente aumentare la frequenza f nel rapporto tra le tensioni di prova e quella nominale. Lo schema di principio è quello indicato nella figura 3.22. Si noti che in questo caso, alimentando da un lato qualsiasi la macchina, si provano contemporaneamente entrambi gli avvolgimenti. La tensione di prova è di regola 2 volte la tensione nominale e deve essere mantenuta per non meno di 15 s.

3.13 – Autotrasformatori
Generalità
Sono trasformatori in cui primario e secondario sono riuniti in un solo avvolgimento, del quale una parte rimane comune al primario ed al secondario. La parte di avvolgimento che appartiene soltanto al primario (o soltanto al secondario) si denomina avvolgimento serie, l’altra parte si dice avvolgimento comune.

In base alla definizione sopra riportata, discendendo subito due caratteristiche fondamentali dell’autotrasformatore:
1- la parte comune è percorsa da una corrente che è la differenza fra le correnti primaria e secondaria;
2- vi è continuità metallica fra la rete primaria e la rete secondaria.

Figura 3.23 – Schema di principio di autotrasformatore: a = abbassatore; b = elevatore.

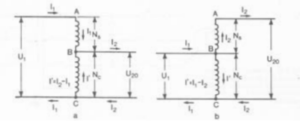
Se si osserva, ad esempio, la figura 3.23a (che si riferisce ad un autotrasformatore abbassatore), si vede che il primario è costituito dalla somma delle spire N_s comprese fra A e B (avvolgimento serie) e delle spire N_c comprese fra B e C; il secondario è formato soltanto dalle N_c spire comprese fra B e C (avvolgimento comune). Si avrà dunque, adottando i simboli usati fin qui per i trasformatori, che il rapporto di trasformazione è dato da:

La porzione di avvolgimento comune BC è, come abbiamo detto, percorsa soltanto dalla differenza delle due correnti primaria e secondaria; esse, infatti, hanno senso opposto: la corrente che circola nella parte comune sarà dunque: I’ = I₂ – I₁

e quindi assai minore di quella che circolerebbe negli avvolgimenti di un trasformatore di tipo normale. Questo fatto porta alle seguenti conseguenze:
1- si realizza una notevole economia di materiale rispetto ad un trasformatore normale in quanto l’avvolgimento primario comprende meno spire, essendo parzialmente costituito dalle spire dell’avvolgimento secondario, ed inoltre la parte comune del l’avvolgimento potrà essere formata con conduttore di sezione molto minore di quella necessaria per un trasformatore di pari potenza;
2- le perdite nel rame e le cadute di tensione nell’avvolgimento comune, essendo determinate dalla corrente I’, sono anch’esse molto minori e quindi anche il rendimento è maggiore di quello di un trasformatore di uguale potenza.

Potenza nominale e di dimensionamento
Per gli autotrasformatori si considerano due potenze: la potenza passante o nominale e la potenza di dimensionamento.

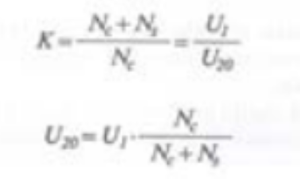
La potenza passante (A_N) è data dal prodotto della tensione a vuoto per la corrente di linea di uno qualunque dei due gruppi di terminali A_N = U_1N · I_1N = U_2N · I_2N. Essa è cioè la potenza nominale, quella che interessa l’impiego e alla quale cisi deve riferire per le ordinazioni. La potenza di dimensionamento (A_d) riguarda invece il costruttore: essa corrisponde a quella che avrebbe un trasformatore ad avvolgimenti separati avente uguali dimensioni dell’autotrasformatore. Questa potenza è data dalla relazione:

Il rapporto (U_1N – U_2N) / U_1N si chiama fattore di riduzione o corapporto. Come si vede dalla formula, la potenza di dimensionamento dell’autotrasformatore dipende dalla differenza fra le due tensioni primaria e secondaria (U_1N – U_2N). Se i valori delle due tensioni sono assai prossimi fra loro, il numeratore della frazione che indica il fattore di riduzione (U_1N – U_2N) / U_1N avrà un valore notevolmente inferiore al valore del denominatore.

Ne consegue che tanto più piccolo è il fattore di riduzione tanto minore sarà la potenza di dimensionamento rispetto alla potenza passante. È evidente che se U_1N fosse uguale a U_2N il fattore di riduzione sarebbe zero e nulla risulterebbe pure la potenza di dimensionamento. In altri termini, l’autotrasformatore non trasferirebbe potenza e quindi non vi sarebbe alcun motivo di ricorrere ad esso. Questi concetti possono essere chiariti con alcuni esempi. Si consideri un autotrasformatore previsto per una potenza nominale (ossia passante) di 600 VA con tensione primaria di 260 V e secondaria di 220 V. La potenza di dimensionamento dell’autotrasformatore, risulta allora:

Questo significa che l’autotrasformatore può essere dimensionato come se fosse un trasformatore da 92 VA. È superfluo rilevare come un trasformatore da 92 VA abbia dimensioni e pesi notevolmente inferiori a quelli di un trasformatore da 600 VA. È facilmente intuibile il risparmio che si consegue adottando un autotrasformatore in luogo di un trasformatore. Come secondo esempio, si consideri un autotrasformatore con tensioni primaria di 500 V, e secondaria di 125 V, la potenza di dimensionamento sarebbe:

Come si vede, il divario delle due potenze (600 VA e 450 VA) è assai minore che nel caso precedente quindi anche il risparmio che si potrebbe conseguire ricorrendo ad un autotrasformatore diminuirebbe molto. Diventerebbe quasi insignificante, ad esempio, se l’autotrasformatore dovesse essere previsto con tensione secondaria an cora più bassa.

Tutte le considerazioni fin qui fatte valgono anche per l’autotrasformatore elevatore. Gli autotrasformatori possono anche essere trifasi e sono sempre collegati a stella in quanto il collegamento a triangolo dà luogo a uno spostamento di fase fra primario e secondario e consente solo un campo limitato di rapporti di trasformazione. Per queste unità la potenza nominale è data dalla relazione: A_N= 1,732 · U_N · I_N
I vantaggi sopra ricordati si contrappongono però alcuni aspetti negativi. Come rilevato, negli autotrasformatori esiste la continuità metallica fra il primario e secondario. Si può osservare innanzitutto che un eventuale guasto a terra di una fase sul lato alta tensione può esporre l’operatore che tocchi un conduttore di bassa tensione ad un potenziale elevato, con pericolo quindi per l’incolumità personale (Figura 3.24). In secondo luogo esiste il problema dell’isolamento dei due avvolgimenti. Se la differenza fra le due tensioni non è rilevante il problema non presenta aspetti particolari, ma se tale differenza è notevole è necessario prevedere l’avvolgimento di bassa tensione per lo stesso livello di isolamento dell’avvolgimento di alta tensione.
È opportuno infine accennare ad un particolare tipo di autotrasformatore adatto a variare con continuità la tensione da zero al valore di rete e che viene usato sovente in laboratorio. Per questa funzione specifica l’apparecchio viene denominato variatore di tensione. Sostanzialmente esso si compone di un nucleo magnetico toroidale sul quale è avvolto, per l’intero suo sviluppo, un avvolgimento realizzato con conduttore di rame isolato tramite smalto (Figura 3.25).

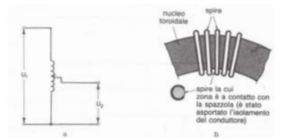
Figura 3.25 – Variatore di tensione monofase a spazzole striscianti: a – schema di principio; b – particolari costruttivi.

In corrispondenza di una delle due facce del toro si provvede a togliere l’isolamento del conduttore e su questa faccia può scorrere una spazzola di grafite che – manovrata tramite apposita manopola – può inserire o disinserire un certo numero di spire, variando in tal modo la tensione ai capi d’uscita dell’apparecchio. La potenza di questi variatori è prevista da poche centinaia di voltampere fino a qualche kilovoltampere. Gli autotrasformatori trifasi a rapporto variabile sono invece costituiti da un nucleo a tre colonne, su ognuna delle quali è avvolta una fase dell’avvolgimento in un solo strato. Tre spazzole di grafite, meccanicamente collegate tra loro da un supporto isolante, scorrono ciascuna su di una fase dell’avvolgimento solitamente collegato a stella (Figura 3.26).

Figura 3.26 – Variatore di tensione trifase a spazzole striscianti.

La potenza nominale può variare da qualche decina fino a qualche centinaia di kilovoltampere.